OpenGL avec Delphi

En quoi les courbes de Bézier peuvent-elles nous être utiles ? Tout d'abord avant de se poser cette question il faut comprendre comment elles fonctionnent et quel en est leur résultat.

• Génération d'un terrain, montagnes.
• Simulation d'éclairs ou d'électricité.
• Diminuer le nombre de sommets utilisés pour réaliser une figure 3D.
• Dessiner des formes géométriques à l'aide de la souris (points de contrôles).

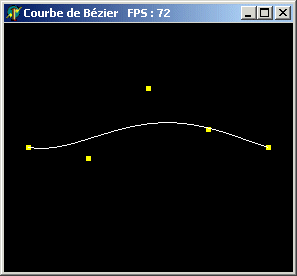
Voici à quoi peut ressembler une courbe de Bézier. Cette courbe-ci est de degré 3 donc 4 points de contrôles. Le degré de la courbe est défini par l'équation suivante n-1, n représentant le nombre de points de contrôles. Ce qui est pratique c'est que l'on positionne nos points de contrôles dans l'espace et ensuite chacun d'eux est relié par une simple ligne, ce qui est appelé l'interpolation. La ligne touche toujours au premier et dernier point de contrôle, mais jamais à ceux entre les deux. Elle ne fait qu'être attirée vers eux. L'inconvénient dans tout cela, c'est que si l'on déplace un point de contrôle alors la ligne risque sévèrement d'être affectée, en raison de l'attirance qu'elle possède envers chacun de ces points. Il existe une autre forme de Courbe nommée B-Spline qui elle permet de déplacer les points de contrôle un à un sans toutefois affecter l'intégrité de la ligne. Mais je ne crois pas en faire un tutoriel.

Points rouges
Ces points sont simplement les points de contrôles de la ligne. Cette courbe en possède quatre. Remarquez que la courbe de Bézier ne touche jamais à ces points de contrôles, à l'exception du premier et du dernier.

Ligne blanche
La ligne blanche représente une droite partant d'un point vers un autre donc du premier vers le deuxième, le deuxième vers le troisième… Celle-ci est seulement visible pour démontrer l'interpolation effectuée par une courbe de Bézier comparativement à une ligne tracée de point en point. On appelle « linéaire » ce type d'interpolation.

Pointillé jaune
Les petits points jaunes sont justement la courbe de Bézier, celle-ci étant attirée vers chacun de ses points de contrôle.

Comme je ne suis pas un génie en mathématiques, je vais me contenter de vous spécifier la mince base des courbes de Bézier, mais ne vous en faites pas je travaille à la réalisation de courbes de Bézier sans l'usage d'OpenGL. Surveillez bien la section Graphique de Delphi.

Avant d'utiliser les courbes de Bézier avec OpenGL, il faut comprendre que la courbe a une vie égale à T = 0..1. Qu'est-ce que tout cela signifie ? Cela veut dire que la courbe débute à son premier point de contrôle, donc T = 0 et termine sont trajet à T = 1 Donc tous les nombres réels inclus à l'intérieur de cet intervalle constituent la précision de la courbe. La courbe située sur la photo en haut, a été réalisée avec une précision de 100, ce qui signifie que sa création a suscité 100 itérations (incluses entre 0 et 1). Si vous ne saisissez pas, ne vous en faites pas vous comprendrez avec l'exemple à la fin du tutoriel.

Comment réaliser une courbe de Bézier à l'aide d'OpenGL. Premièrement nous avons besoin de cette commande-ci pour définir un évaluateur :glMapX. Le « x » à la fin signifie que nous pouvons traiter des courbes 1D, 2D et 3D. Cette fonction requiert un pointeur vers un tableau de points de contrôle et une valeur indiquant le nombre de points de contrôle situé dans le tableau. Mais avant d'utiliser cette commande, nous devons l'actionner à l'aide de glEnable( GL_MAP1_VERTEX_3 ). Voici un petit bout de code :

Type
    TPtrCtrl = Array[0..4, 0..2] Of TGLfloat;

Var
   PointsDeCtrl : TPtrCtrl =(
                    ( -10.0,  0.0, 0.0 ),
                    (  -5.0, -5.0, 0.0 ),
                    (   0.0,  7.0, 0.0 ),
                    (   5.0,  5.0, 0.0 ),
                    (  10.0,  0.0, 0.0 ) );

TPtrCtrl
Voici le tableau de points de contrôle. Il renferme quatre points de contrôle spécifiés sous le format XYZ.

Pour que l'évaluateur évalue la courbe, nous devons en faire la demande à l'aide de la commande suivante : glEvalCoord. Cette commande requiert un degré de précision entre 0..1.

Chaque fois que les coordonnées des points de contrôle changent alors il suffit d'appeler la commande glEvalCoord pour que la courbe soit réévaluée. Alors si les points se déplacent constamment, il serait mieux d'appeler cette commande dans notre procédure d'affichage.

glMap1f( GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 5, @PointsDeCtrl );

     glColor4f( 1.0, 1.0, 1.0, 1.0 );
     glBegin( GL_LINE_STRIP );
        For I := 0 To 20 Do
        Begin
             glColor4f( 1.0, 1.0, 1.0, 1.0 );
             glEvalCoord1f( I / 20.0 );
        End;
     glEnd();

      glPointSize( 5.0 );
      glColor4f( 1.0, 1.0, 0.0, 1.0 );
      glBegin( GL_POINTS );
         For I := 0 To 4 Do
             glVertex3f( PointsDeCtrl[I, 0], 
                         PointsDeCtrl[I, 1], 
                         PointsDeCtrl[I, 2] );
      glEnd();

glBegin( GL_LINE_STRIP )..glEnd();
Dans cette boucle, nous évaluons la courbe de Bézier avec une précision de 20.

glBegin( GL_POINTS )..glEnd();
Cette boucle-ci sert à tracer les points de contrôles, elle est optionnelle.

La création d'un compteur de cadre est assez simple si l'on part du fait que l'on doit calculer combien de fois une scène est affichée en une seconde. Tout d'abord il faut mettre sur pied un compteur, mais comment ? Simple en servant de la fonction SetTimer et de notre fenêtre OpenGL comme cible du Timer. Ensuite pour intercepter le timer, il nous suffit de capter le message envoyé à notre fenêtre WM_TIMER. Le timer doit être démarré avec un intervalle de 1000 millisecondes donc 1 seconde.

Source

Remarquer l'attirance de la courbe vers chacun de ses points de contrôles. Voici deux petites choses à essayer :

• augmenter le nombre de points de contrôle ;
• augmenter la précision de la courbe de Bézier.