OpenGL avec Delphi

Dès qu'on parle de transformation cela sonne aussi ANIMATION. Comme je ne suis pas très très fervent du TTimer de Delphi je vous propose un Timer beaucoup plus rapide. J'espère que vous comprendrez bien sinon ne vous gênez pas pour les questions.

Pour ceux qui utilisent la manière (à la C++) du premier tutoriel alors vous n'avez pas besoin de ce TIMER.

Qu'est-ce que les transformations, il s’agit par exemple de faire effectuer une rotation, une translation ou encore un changement d'échelle à une primitive. Dans ce tutoriel nous verrons les principales commandes qui permettent d'effectuer ces transformations.

Voici ce que vous devez inclure dans l'événement OnPaint() de votre fenêtre.

glClear(GL_COLOR_BUFFER_BIT);
glClearColor(0.0, 0.0, 0.0, 0.0);

glMatrixMode(GL_MODELVIEW);
glLoadIdentity;

gluLookAt( 0.0, 0.0, 20.0,
           0.0, 0.0, 0.0,
           0.0, 1.0, 0.0 );

     glPushMatrix();
          glScaled( Redim, 1.0, 1.0 );
          glRotated( DegreRot, 0, 0, 1 );
          glTranslated( Redim, 0.0, 0.0 );

          glBegin( GL_TRIANGLES );
              glColor3f( 1.0, 1.0, 1.0 ); glVertex2d(  2.0, -2.0 );
              glColor3f( 0.5, 0.5, 0.0 ); glVertex2d( -2.0, -2.0 );
              glColor3f( 0.0, 0.5, 0.5 ); glVertex2d(  0.0,  2.0 );
          glEnd();
     glPopMatrix();

glFlush;

Explication de ce bout de code :

glPushMatrix(); / glPopMatrix();

Vous verrez que ces deux commandes sont plus qu'utiles quand on possède plus d'une primitive dans notre scène. Tout d'abord il faut comprendre que chaque transformation que l'on effectue est stockée sous forme de matrice (4 x 4). glPushMatrix permet de sauvegarder la matrice active et glPopMatrix permet de récupérer la matrice précédemment sauvegarder. Ces deux commandes fonctionnent de la même manière que la pile d'un ordinateur donc comme une pile d'assiettes (LIFO : Last In First Out). Mais pourquoi cela peut être utile et bien voilà une petite exemple.

Voici deux primitives que vous devez utiliser pour construire une roue de voiture.

                                                 + =

Attention : prenez par exemple un des triangles positionnés sur l'image résultat, constatez-vous qu'il ne possède plus le même angle que sur l'image 2 ? Si vous avez remarqué alors c'est que vous avez compris aussi que ces triangles ont tous subi un effet de rotation de x degrés. Cette rotation s'effectuera avec la commande glRotate*(). Maintenant je vous donne la manière de procéder pour dessiner cette roue tout en faisant effectuer une rotation triangle par triangle sans jamais affecter l'ensemble des autres éléments dans la scène ou plutôt de la roue elle-même. Malgré que la roue elle-même soit ronde alors une rotation sur celle-ci n'aurait pas grande importance, mais c'est la seule idée qu'y m'est venue en tête au moment où j'ai conçu ce tutoriel.

1. Dessiner la roue.
2. Sauvegarder la matrice.
3. Rotation du triangle #1.
4. Dessin du triangle #1 sur la roue.
5. Récupération de la matrice.
6. Sauvegarder la matrice.
7. Rotation du triangle #2.
8. Dessin du triangle #2 sur la roue.
9. Récupération de la matrice.
10. Sauvegarder la matrice.
11. Rotation du triangle #3.
12. Dessin du triangle #3 sur la roue.
13. Récupération de la matrice.

De cette manière vous vous assurez que les transformations effectuées sur des primitives entre ces deux commandes glPushMatrix() et glPopMatrix() n'affectent que les primitives c'est primitives et non ceux à l'extérieur. Pratique non ?

glTranslate*(x, y, z);

Comme son nom l'indique cette commande effectue une translation dans un axe donné selon X, Y ou Z. Même si l'image semble rétrécir ne croyez pas que le carré change d'échelle, mais il se translate simplement vers l'axe des Z donc en profondeur.
Voici l'explication graphique :

glRotate*(Angle, x, y, z );

Encore une fois son nom ne ment pas : cette commande sert à effectuer des rotations selon un axe et un angle donné. Mais ici il faut faire attention, car cela dépend si une translation a été appelée avant ou après, cela peut entrainer des transformations différentes. Voici la différence si l'on exécute une translation suivie d'une rotation et le cas contraire :

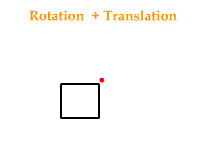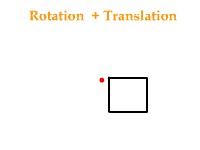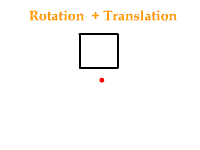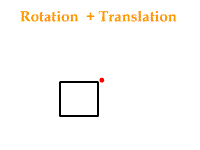
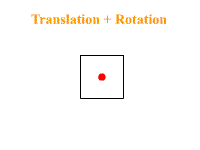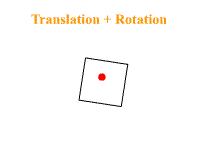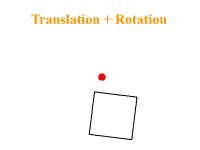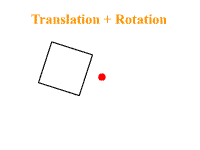
glScale*( x, y, z );

Commande permettant d'effectuer des redimensions sur une primitive selon l'axe donné. Si la valeur donnée est < 1 alors la primitive sera réduite sinon si la valeur donnée est > 1 alors la primitive sera grossie. Si la valeur est égale à 1 alors rien ne se produit. Explication graphique :

Capture d'écran :

Je m'excuse encore pour ma roue de voiture je sais que c'est vulgaire et dégueulasse, mais il faut dire que je ne suis pas un as en art plastique. Amusez-vous à interchanger les commandes de transformation et essayez de remarquer les différences que cela provoque. Si c'est trop facile alors vous pouvez toujours ajouter une autre primitive et contrôler les transformations d'une et l'autre avec les deux commandes magiques : glPushMatrix(); et glPopMatrix(); Source

Pour ceux que intéresse, voici l'autre manière. Source (à la C++)